The 2-Tissue (BFM) model implements fitting a two-tissue compartment model in each image pixel. It is based on an analytic solution of the system of differential equations which results in the calculation of two eigenvalues α1 and α2.
![]()
The expected tissue activity is obtained by the convolution of the input function with a sum of two decaying exponentials plus a contribution from whole blood.
![]()
This operational equation which can be fitted to the data has 5 parameters: θ1, θ2, α1, α2, vB . It is linear in the parameters θ1, θ2, vB, and nonlinear in α1, α2 . The θ1 and θ2 parameters are also a combination of the rate constants.
The basis function method by Hong and Fryer [1] performs the data fitting in the following way:
1.For a certain tracer the physiological range of k2, k3, k4 can be determined. These values can be translated into a range of α1 and α2 values which can be expected in the data. With FDG, for instance, α1∈[0.0005,0.015]min-1 and α2∈[0.06,0.6]min-1.
2.The functions ![]() and
and ![]() are called the basis functions. They are pre-calculated for tabulated α1 and α2 values which span the prescribed ranges.
are called the basis functions. They are pre-calculated for tabulated α1 and α2 values which span the prescribed ranges.
3.In fitting the data, each combination of α1 and α2 is examined: the operational equation is fitted using the two corresponding basis functions with respect to the remaining parameters θ1, θ2, vB. Since all of them enter linearly, the solution is unique and can be quickly calculated. For each of the calculations the chi-square criterion is recorded.
4.Since the fitting has to be performed for each combination of α1 and α2, N2 results are obtained if N is the number of table entries. Finally the combination θ1, θ2, vB, α1, α2 with minimal chi square is considered as the solution.
In the case of irreversible binding k4 is assumed to be zero. Hereby the number of fitted parameters is reduced and the operational equation simplifies to
![]()
It is notable that in this case only one basis function appears in the equation. Therefore, the number of linear fits is reduce from N2 to N, making pixelwise fitting very fast.
Overview of the BFM Processing in PXMOD
In PXMOD, both the reversible and the irreversible configuration are supported. Furthermore, it is possible to allow fitting of the blood volume fraction, or to fix it at a specific value. The linear fitting is done without weighting using the singular value decomposition method.
The configurations (k4 fitted or 0, vB fitted or fixed) are specified as parameters of preprocessing. During preprocessing, the 2xN basis functions are pre-calculated and stored for pixelwise processing. Then, the BFM analysis is applied to the TAC and the result shown for inspection. Finally, pixelwise processing calculates maps of all parameters.
In setting up the processing for a new tracer it is recommended to enable the calculation of the α1 and α2 maps and inspect them regarding the prescribed range. If the prescribed maximum or minimum value is very frequently encountered this indicates that the range should be expanded.
Acquisition and Data Requirements
Image Data |
A dynamic PET data set. |
Blood Data |
Input curve from the time of injection until the end of the acquisition. |
Blood Preprocessing
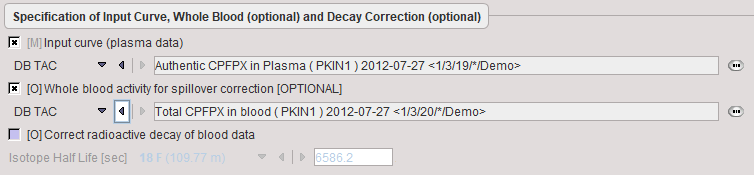
Data to be provided are the input curve, and optionally a whole-blood TAC for spillover correction. No whole-blood curve is defined, the input curve will also be used for spillover correction.
Model Preprocessing
During model preprocessing the basis functions are calculated for the prescribed range of α1 and α2 values. The default ranges α1∈[0.0005,0.015]min-1 and α2∈[0.06,0.6]min-1 are suitable for FDG. To change the ranges please first enable the alpha1 or alpha2 parameter and then adjust the Lower and Upper values.
Also important is the fit flag of vB and k4. If vB is checked, the blood fraction will be fitted in model preprocessing and also in the map calculation. Otherwise, the specified value will be used for spillover correction. If k4 is checked, the full 2-tissue compartment model with four parameters will be fitted in model preprocessing and map calculation. Otherwise, the specified value will be disregarded and k4 set to zero in all fits.
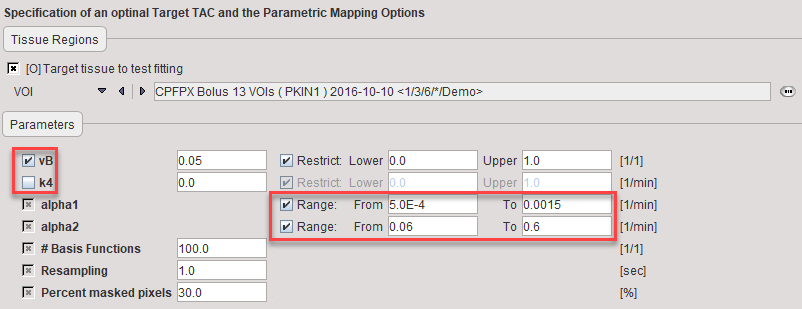
vB |
Blood volume fraction. Can be fitted or fixed. |
k4 |
Rate constant k4 in the 2-tissue compartment model. Can be fitted, otherwise it is set to 0. |
alpha1, alpha2 |
First and second eigenvalue. The Lower/Upper values are used for defining the basis function ranges. |
#Basis Functions |
Number of intermediate αi values generated between Lower and Upper. The increments are logarithmically spaced. |
Resampling |
Sampling increment applied during the basis function calculation. |
Percent masked pixels |
Exclude the specified percentage of pixels based on histogram analysis of integrated signal energy. Not applied in the presence of a defined mask. |
Model Configuration
The example below shows a typical configuration for an irreversible mode (k4 = 0 fixed)
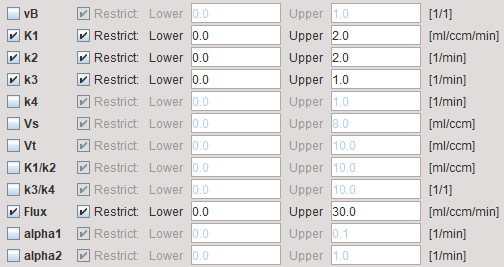
vB |
Blood volume fraction defining the pixelwise blood spillover correction. To fit, please activate in the Preprocessing tab. |
K1,k2,k3 |
Rate constants of the 2-tissue compartment model. |
k4 |
Rate constant of the 2-tissue compartment model. A map can only be obtained if k4 has been checked for fitting in the preprocessing configuration. Otherwise the map will be zero. |
Vs |
Distribution volume of the second compartment. It is only defined for a reversible configuration where k4 has been checked for fitting. |
Vt |
Distribution volume. |
K1/k2 |
Distribution volume of the non-displaceable compartment. |
k3/k4 |
Binding potential of receptor tracers. |
Flux |
Influx of the tracer, also called Ki. |
alpha1, alpha2 |
Shows the α1 and α2 values of the found solution. These values can be used to check whether the defined range was adequate. |
Reference
1.Hong YT, Fryer TD: Kinetic modelling using basis functions derived from two-tissue compartmental models with a plasma input function: general principle and application to [18F]fluorodeoxyglucose positron emission tomography. Neuroimage 2010, 51(1):164-172. DOI