In addition to uptake and washout the model handles two exchanging compartments C1 and C2 in tissue.
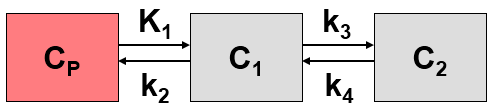
Differential Equation of the Mass Balance
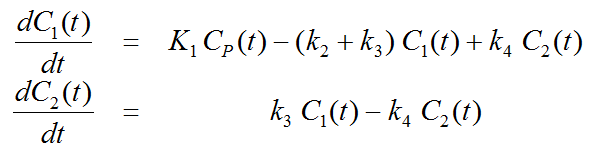
with input curve Cp(t).
Operational Model Curve
With linearized solutions, the differential equations are integrated twice on both sides, substitutions performed and finally rearranged. This can be done in different ways. The current model uses the derivation of Cai et al. [1], equation (6):
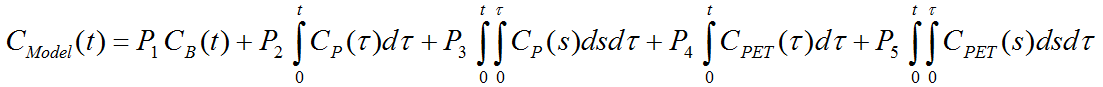
with input curve Cp(t), the concentration CB(t) of tracer in whole blood, and the tissue curve to be fitted CPET(t).
Parameter Fitting
The multi-linear operational equation can be solved in a least squares sense in one step using a singular value decomposition method. From the resulting 5 coefficients P1, .. , P5 the target parameters can be calculated as follows:
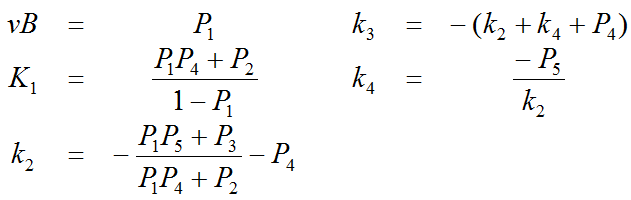
Recommended Use of the Linear Least Squares Method
The advantages of the linearized approach are fast computation, a well-defined solution, and no problem with local minima. However, it is well known that the method is susceptible to bias, and that small TAC perturbations can cause large changes of the parameter estimates. Therefore it is recommended that the Linear Least Squares model is only used for getting a quick solution which is further refined by the iterative methods. In fact, if Parameters Initialization option is configured in the Extras panel, the initial starting parameters of the compartment models are obtained by the Linear Least Squares method.
Implementation Notes
The model works as follows for different model configurations:
▪Irreversible model: if k4 is disabled from fitting, the program automatically sets k4 = 0 and uses a linearized equation which is modified accordingly.
▪1-tissue compartment model: if k3 is disabled from fitting, the program automatically sets k3 = k4 = 0 and uses a modified equation.
▪In all configurations the vB parameter can optionally be disabled from fitting and fixed at a specific user-defined value.
Reference
1.Cai W, Feng D, Fulton R, Siu WC: Generalized linear least squares algorithms for modeling glucose metabolism in the human brain with corrections for vascular effects. Comput Methods Programs Biomed 2002, 68(1):1-14.