The Vt (3 Calc Methods) model is a convenience model for calculating the total distribution volume of reversible receptor tracers with three different methods:
1.the Logan Plot method [1] with standard linear regression (yielding Vt_logan),
2.the Logan Plot with a linear regression based on the perpendicular distances [2] (Vt_perpend),
3.Ichise's MA1 bilinear method [3] (Vt_ma1)
Logan Plot
The Logan plot has been developed by Logan et al. [1] for ligands that bind reversibly to receptors and enzymes and is used for estimating the total distribution volume VT. Its results can be interpreted with respect to the 1- and 2-tissue compartment models.
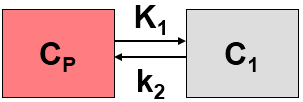
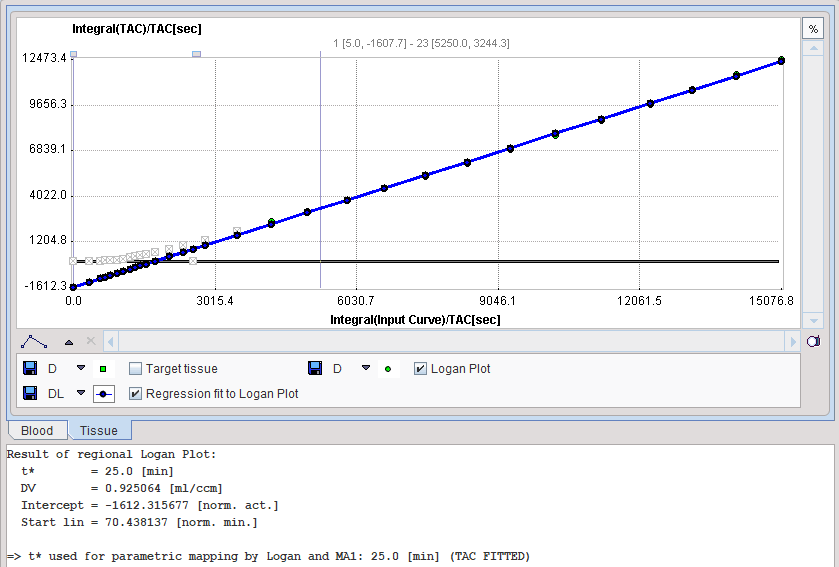
The Logan plot belongs to a group of Graphical Analysis techniques, whereby the measured tissue TAC CT(T) undergoes a mathematical transformation and is plotted against some sort of "normalized time". The Logan plot is given by the expression
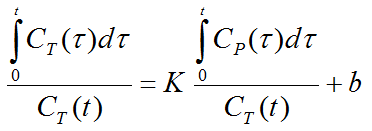
with the input curve Cp(t). This means that the tissue activity integrated from the time of injection is divided by the instantaneous tissue activity, and plotted at a "normalized time" (integral of the input curve from the injection time divided by the instantaneous tissue activity). For systems with reversible compartments this plot will result in a straight line after an equilibration time t*.
In the derivation of the Logan plot the PET signal is described as a sum of tissue activity plus a fractional plasma signal
![]()
unlike the operational equation of the compartment model. Under these premises the slope represents the total distribution volume VT plus the plasma space vP in the VOI, which is usually neglected. Therefore
![]()
It has been found that the Logan plot is susceptible to noise in the data. Noise causes the true VT to be underestimated, to a degree which not only depends on the noise level, but also on the local kinetics. The underestimation problem is particularly relevant in parametric mapping, where the pixelwise TACs suffer from a high noise level.
The reason for the underestimation effect is the fact that noise is not only present in the y-values (dependent variable) as the linear regression assumes, but also in the x-values (independent variable). To arrive at more accurate results it was therefore proposed to measure the residuals perpendicular to the regression line, rather than vertical to the x-axis [2].
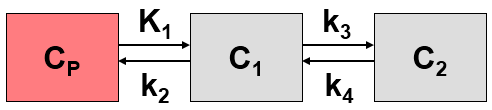
Ichise's MA1 Method
Ichise's MA1 analysis method [3] is a further development of the Logan plot aimed at minimizing the bias induced by noise in the measurements.
The following bilinear relationship was derived
![]()
where CT(t) represents the tissue time-activity curve, CP(t) the plasma activity, VT the total distribution volume, and b the intercept of the Logan plot which becomes constant after an equilibration time t*.
Based on simulation and experimental data the authors show that MA1 demonstrates the largest bias reduction among several methods. Therefore they conclude, that MA1 is the method of choice for calculating the total distribution volume, if t* can accurately be defined.
Acquisition and Data Requirements
Image Data |
A dynamic PET data set. |
Blood Data |
Input curve from the time of injection until the end of the acquisition. |
Tissue TAC |
Optional: A regional time-activity curve from a representative tissue region. It is presented as a Logan plot and can be used to define the linear segment where regression analysis should be done. |
Blood Preprocessing
Decay correction is the only blood correction option.

Model Preprocessing
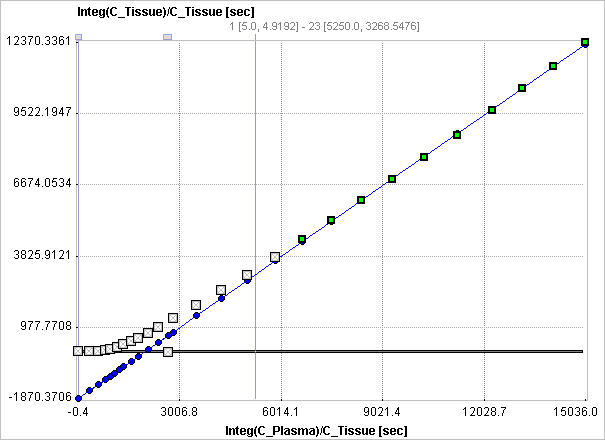
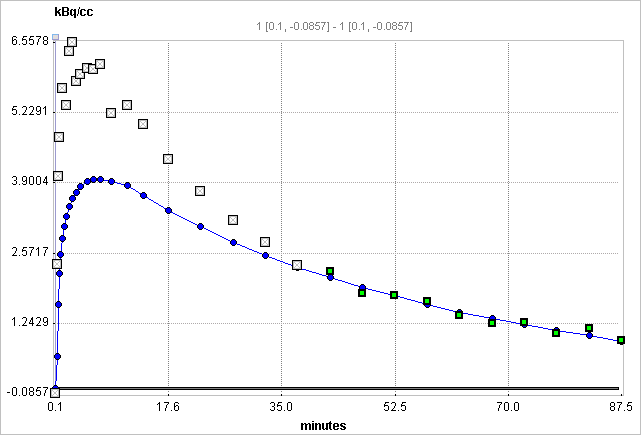
If a tissue VOI (Target tissue) is configured, the Logan graphical plot is performed and presented to the user. In this plot, the data should become linear after an equilibration time. The slope of the linear segment equals the total distribution volume. The user must decide on the beginning of the linear segment and specify this time (which is NOT in acquisition time) in the model configuration. An alternative is to apply an automatic criterion for determining this start time.
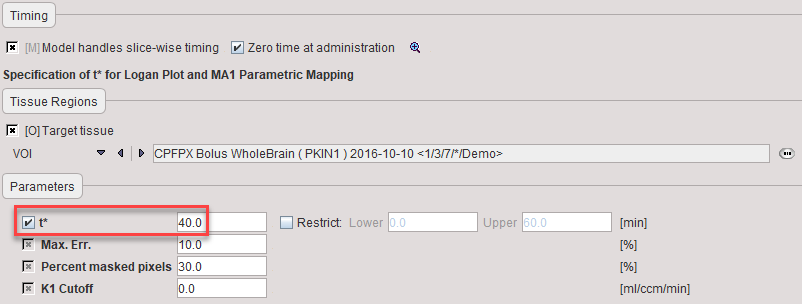
t* |
The linear regression estimation should be restricted to a range after an equilibration time. t* marks the beginning of the range used in the multi-linear regression analysis. It can be fitted based on the Max. Err. criterion. Note that the t* is in acquisition time. |
Max Err. |
Maximum relative error ( (measured-predicted)/predicted ) allowed between the linear regression and the Logan-transformed measurements in the segment starting from t*. |
Percent masked pixels |
Exclude the specified percentage of pixels based on histogram analysis of integrated signal energy. Not applied in the presence of a defined mask. |
K1 Cutoff |
Threshold value of K1 calculated with the MA1 method. In pixels with K1 smaller than the cutoff all MA1-related parameters are set to NaN. |
The Logan plot is shown in the preprocessing Model Results panel. The user should consult this plot in order to check whether the Start time is adequate.
Model Configuration
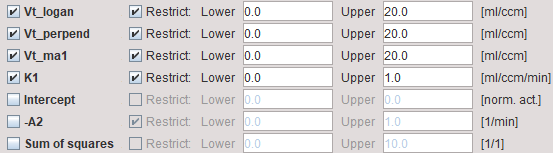
The regressions in pixelwise processing (all 3 methods) only use the data segment determined by Start Lin in the Model Pre-Processing area.
Vt_logan |
Total distribution volume calculated with standard Logan plot. |
Vt_perpend |
Total distribution volume calculated with the Logan plot using perpendicular distances. |
Vt_ma1 |
Total distribution calculated using Ichise's MA1 method. This method has less bias, but more variance and the maps often are contaminated by outliers. |
K1 |
First regression coefficient of the MA1 method. If the kinetics can be described by a 1-Tissue compartment model, it provides a relative "perfusion" image which may be helpful for the anatomical correlation or matching. If a 2-Tissue compartment model is required to describe the kinetics, it corresponds to K1*(1+k3/k4). |
Intercept |
y-Intercept of standard regression line. |
-A2 |
Second regression coefficient of the MA1 method. |
Sum of squares |
Sum of squared differences for the Logan plot. |
References
1.Logan J, Fowler JS, Volkow ND, Wolf AP, Dewey SL, Schlyer DJ, MacGregor RR, Hitzemann R, Bendriem B, Gatley SJ et al: Graphical analysis of reversible radioligand binding from time-activity measurements applied to [N-11C-methyl]-(-)-cocaine PET studies in human subjects. J Cereb Blood Flow Metab 1990, 10(5):740-747. DOI
2.Varga J, Szabo Z: Modified regression model for the Logan plot. J Cereb Blood Flow Metab 2002, 22(2):240-244. DOI
3.Ichise M, Toyama H, Innis RB, Carson RE: Strategies to improve neuroreceptor parameter estimation by linear regression analysis. J Cereb Blood Flow Metab 2002, 22(10):1271-1281. DOI