<< Click to Display Table of Contents >> Navigation:  R Statistics in PMOD > Analysis Scripts for Aggregates > Test-Retest

Once a quantitative methodology has been established, the variability of the outcome parameters needs to be assessed in order to find out, what effect sizes can be detected.

Test-Retest Variability and ICC

A test-retest study should be performed with about 10 subjects to evaluate the variability of the relevant outcome parameters. Each subject is studied twice, whereby the physiological and experimental conditions should be as similar as possible. Due to biologic variability, both acquisitions are preferably done on the same day.

The data quantification method in question is applied for all regions of interest and the results from all subjects pooled. The test-retest variability (VAR, also called within subject variability) is then calculated for each region as follows:

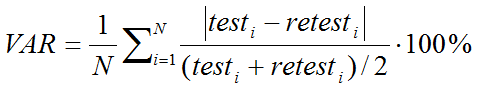
where N represents the number of subjects and testi and retesti the result values of the quantification method. Hence, the test-retest variability represents the average percent difference of the regional results across the subjects. As an example, the variability of the macro-parameters (Vt, BPND) in PET is typically in the range of about 5–10%. Brain perfusion is known to be subject to significant physiological variability, and therefore has 20% test-retest variability.

The same data can be used to calculate the variability across the study population. This between-subject variability for a specific region is defined as the coefficient of variation BS(%COV) of the outcome across the population, hence

where SD represents the standard deviation of the results across subjects.

Another important measure which can be calculated from test-retest data is the intraclass correlation coefficient (ICC). It estimates the reliability of the measurement per region by comparing the within-subject (WS) variability to the between-subject (BS) variability. For the test-retest situation it can be calculated as follows:

whereby the MSS represents mean sum of squares and is calculated for the WS and the BS situation by

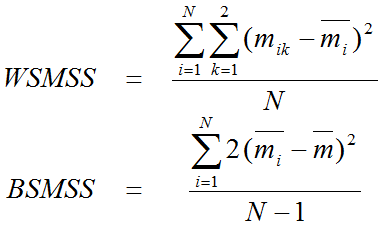
represents a result of subject i (k=1 test, k=2 retest), the test-retest mean of subject i, and the overall mean across all studies and subjects.

Expected ICC values range between 0 (no reliability) and 1 (maximum reliability, achieved in the case of identity between test and retest). However, in certain circumstances even negative ICC values may occur in actual data sets (indicating no reliability): particularly, in case more differences are observed within than between subjects.  

ICC values reflect the relation between measurement reproducibility and the spread of target values. They are commonly considered excellent above 0.75 and acceptable when ranging between 0.5 and 0.75.

See [1] for an application in PET modeling.

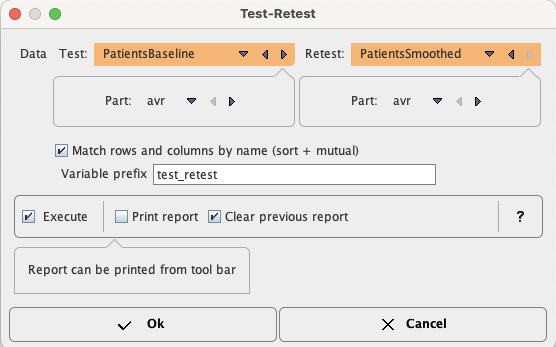
Test-Retest Configuration

The Test-Retest script performs the calculations described above between two variables in the workspace for all VOIs. The only choices in the user interface are the Data variables, and the statistics within the variables (Part)

Test-Retest Results

This script only provides a result table Test_Retest_Result

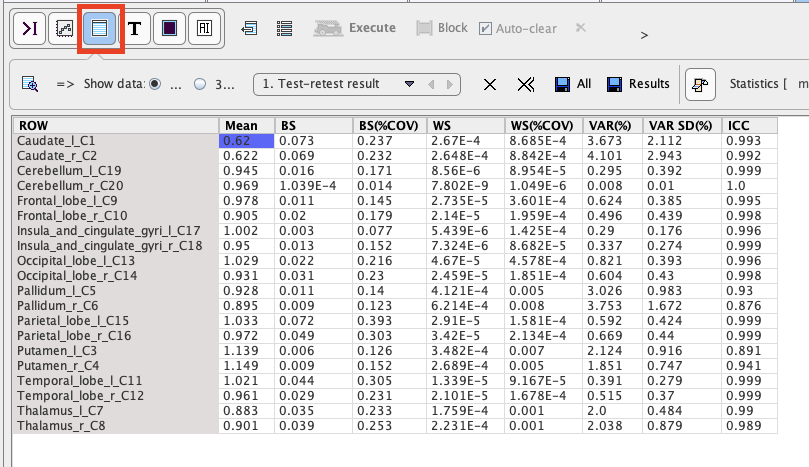
with the following results per VOI:

References

1.Parsey RV, Slifstein M, Hwang DR, Abi-Dargham A, Simpson N, Mawlawi O, Guo NN, Van Heertum R, Mann JJ, Laruelle M: Validation and reproducibility of measurement of 5-HT1A receptor parameters with [carbonyl-11C]WAY-100635 in humans: comparison of arterial and reference tissue input functions. J Cereb Blood Flow Metab 2000, 20(7):1111-1133. DOI

2.Weir JP: Quantifying Test-Retest reliability using the intraclass correlation coefficient and the SEM. J. Strenght Cond. Res. 2005, 19(1): 231-240